Дяків Віра Іванівна
Дяків Віра Іванівна
вчитель математики
 Перевернутий клас (англ. flipped classroom) - принцип навчання, за яким основне засвоєння нового матеріалу учнями відбувається вдома, а час аудиторної роботи виділяється на виконання завдань, вправ, проведення лабораторних і практичних досліджень, індивідуальні консультації вчителя тощо. Принцип був запропонований у 2007 році учням Вудландської школи в штаті Колорадо (США) двома вчителями природничих наук - Джонатаном Бергманом та Аароном Самсом. Вони почали створювати короткі відео з матеріалами лекцій, які учні мали переглядати вдома. Уроки ж присвячувались лабораторним роботам, а також відповідям на питання від учнів.
Перевернутий клас (англ. flipped classroom) - принцип навчання, за яким основне засвоєння нового матеріалу учнями відбувається вдома, а час аудиторної роботи виділяється на виконання завдань, вправ, проведення лабораторних і практичних досліджень, індивідуальні консультації вчителя тощо. Принцип був запропонований у 2007 році учням Вудландської школи в штаті Колорадо (США) двома вчителями природничих наук - Джонатаном Бергманом та Аароном Самсом. Вони почали створювати короткі відео з матеріалами лекцій, які учні мали переглядати вдома. Уроки ж присвячувались лабораторним роботам, а також відповідям на питання від учнів.Переваги методу
- Учень отримує знання тоді, коли йому зручно, а не тільки за умови появи на уроці. Це може бути і відео, завантажене на смартфон чи планшет, аудіолекція, завантажена на плеєр.
- Учень засвоює матеріал у своєму темпі, може подивитися відео або прослухати аудіо стільки, скільки вважає за потрібне, зробити паузу для конспекту або простого сприйняття нової інформації.
- Формат індивідуальних консультацій з учителем допомагає дітям позбутися фрустрації і страху не зрозуміти новий матеріал. Це також допомагає вчителю бачити прогрес і рівень розуміння кожного окремого учня.
- На уроках час не витрачається на виклад нового матеріалу, завдяки чому створюється більше можливостей для застосування знань.
- Методика не вимагає спеціальних дорогих технічних пристроїв. Для реалізації роботи в межах "перевернутого класу" може знадобитись звукозаписний пристрій (диктофон, мікрофон), камера або вебкамера, комп'ютер зі стандартним програмним забезпеченням.
- Учні можуть використовувати більшу кількість додаткових джерел при самостійній підготовці вдома: інтернет, домашні книги, словники і т. д.
Презентація
Перевернутий клас на уроках математики
Перетворення графіків тригонометричних функцій
Потрібно знати! (повторення)
Таблиця перетворень графіків функцій
Перевір себе: Графіки елементарних функцій
Перевір себе: Перетворення графіків елементарних функцій
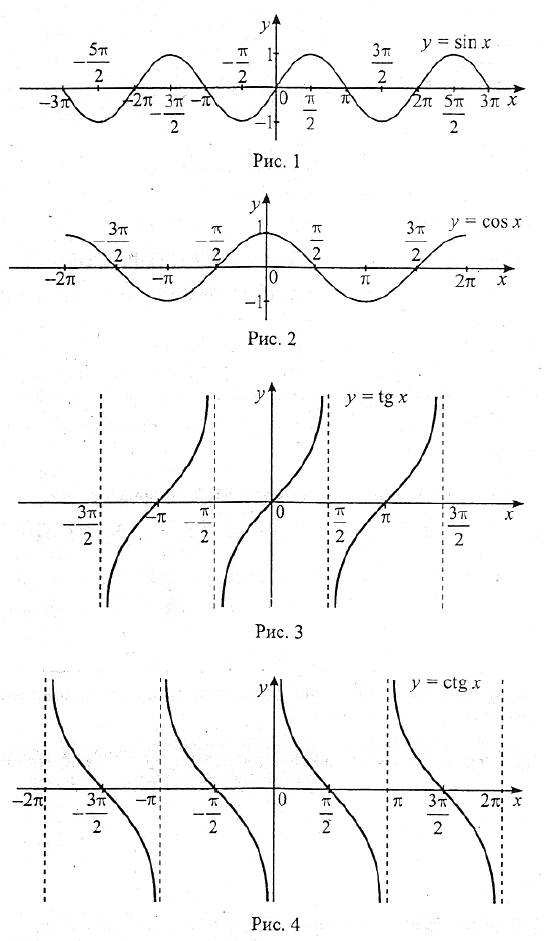
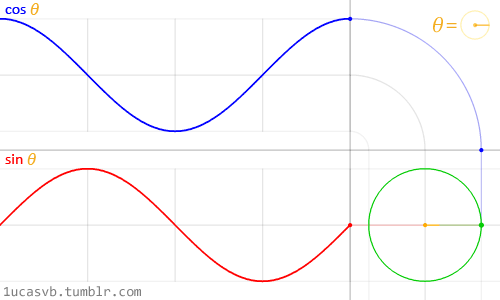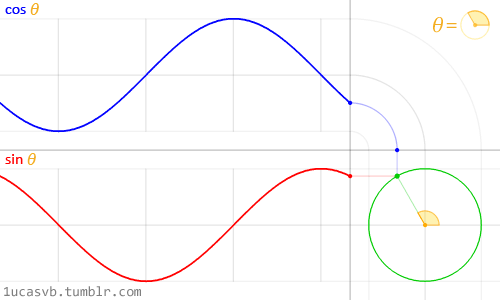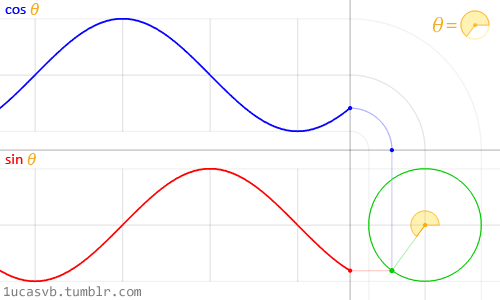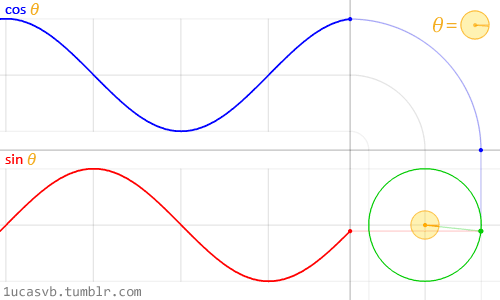
Графіки тригонометричних функцій
Перевір себе: Графіки елементарних функцій
Перевір себе: Перетворення графіків елементарних функцій
Графіки тригонометричних функцій
Превірте свої знання про графіки тригонометричних функцій
А тепер до нової теми!
Перетворення графіків тригонометричних функцій.
Перегляньте уважно відео (1-4), якщо є потреба то декілька раз.
Після кожного відео перевір свої знання, виконавши вправи.
Відео 1. Перетворення y=f(x)+-a і y=f(x+-a)
Перевір себе вправа1
Якщо у вправі було багато помилок, передивись ще раз відео і спробуй зробити ще раз:)
Відео 2. Перетворення y=kf(x) і y=f(кx)
Перевір себе: вправа2
Якщо у вправі було багато помилок, передивись ще раз відео і спробуй зробити ще раз:)
Відео 3. Перетворення y= -f(x) і y=f(-x)
Відео 4. Перетворення y= |f(x)| і y=f(|x|)
111
Для глибшого розуміння, рекомендую спробувати побутувати графіки в он-лайн режимі і розібратись, як буде змінюватись графік, залежно від поставлених коефіцієнтів. Будуємо ТУТ
Можна також переглянути: Всі перетворення разом(презентація)
Приклад відео
Виконайте підсумковий тест (оцінюється)
Оцінювання